Utilizando las transformaciones de equivalencia mencionadas
anteriormente en la resolución de ecuaciones lineales, cualquier ecuación de segundo grado la podemos
transformar en una equivalente que tenga la forma a x2 + b x + c = 0, siendo a distinto de cero.
Las soluciones de una ecuación de la forma a x2
+ b x + c = 0, se obtienen mediante la fórmula siguiente:
Demostración:
Tenemos
que a x2 + b x + c = 0 y queremos encontrar los valores de x que cumplen la
ecuación (sus soluciones).
Multiplicamos los dos miembros de la ecuación
por 4a:
(a x2 + b x + c)· 4a = 0· 4a
4 a2 x2 + 4 a b x + 4 a c = 0
Sumamos b2 a los dos miembros:
4 a2 x2 + 4 a b x + 4 a c + b2 = b2
Restamos 4ac a los dos miembros y, entonces tenemos un cuadrado
perfecto en el miembro izquierdo:
4 a2 x2 + 4 a b x + 4 a c + b2 – 4 a
c = b2 – 4 a c
4 a2 x2 + 4 a b x + b2 = b2
– 4 a c
(2 a x)2 + 4 a b x + b2
= b2 – 4 a c
(2 a x + b)2 = b2 – 4 a
c
Eliminamos el cuadrado de la izquierda extrayendo la raíz cuadrada en ambos
miembros:
Finalmente, despejamos x:
Ejemplo:
Resolvamos la ecuación 3
x2 – 3 x - 18 = 0.
Observamos que a = 3, b = - 3 y c
= - 18.
Sustituimos estos valores en la
fórmula anterior:
Así, las dos soluciones de esta ecuación son x1
= (3 + 15)/6 = 3 y x2 = (3 - 15)/6 = - 2.
La utilización de esta
fórmula es la forma general de resolver cualquier ecuación de segundo grado.
Sin embargo, algunas de las ecuaciones pueden resolverse sin necesidad de
utilizarla. Es el caso de las que se llaman incompletas, aquellas en las que
alguno de los coeficientes b o c es nulo.
Veamos cómo actuar en estos
casos.
Si
b = 0,
la ecuación es de la forma a x2
+ c = 0. Y basta con despejar la incógnita para resolver la ecuación:
a x2 = - c
x2 = - c/a
Y las soluciones de la ecuación serían:
Si
c = 0,
la ecuación es de la forma a x2
+ b x = 0. En este caso, extraemos la incógnita como factor común:
x·(a x + b) = 0
Para que el producto de dos
números sea nulo, alguno de ellos ha de serlo también. Por tanto, o bien es x =
0, o es a x + b = 0.
De aquí podemos deducir que las
soluciones de la ecuación son x1 = 0 y x2 = - b/a.
Ejemplos:
a) Resolvamos 5 x2 – 80 = 0.
En este caso, basta con despejar la incógnita:
5 x2 – 80 = 0
5 x2 – 80 + 80 = 0 + 80
5 x2 = 80
x2 = 80/5 = 16
La soluciones de la ecuación son las raíces cuadradas de 16; es decir, x1
= 4 y x2 = - 4.
b) Resolvamos 8 x2
+ 72 x = 0.
Ahora extraemos la incógnita como
factor común:
x·(8 x + 72) = 0
Las opciones posibles son x = 0, o bien 8 x + 72 = 0. Por tanto, las
soluciones de la ecuación son x1 = 0 y x2 = - 72/8 = - 9.
Número
de soluciones de una ecuación de segundo grado.
Se llama discriminante de una ecuación de segundo
grado, de la forma a x2 + b x + c = 0, al valor de la expresión b2
– 4 a c.
Si nos fijamos en la fórmula
general de resolución de estas ecuaciones, observamos que el valor del
discriminante determinará el número de soluciones de la ecuación.
En efecto, si el discriminante es cero, las
soluciones de la ecuación serán:
Se ve claramente que ambas son iguales y se dice que la ecuación tiene una solución doble.
Si el discriminante es negativo, no existe la raíz cuadrada de dicho valor en el conjunto de los números reales. Por tanto, la ecuación no tiene solución en el conjunto de los reales.
Si el discriminante es positivo, como en los reales existe siempre la raíz cuadrada de un número positivo, la ecuación tendrá dos soluciones reales distintas que son las siguientes:





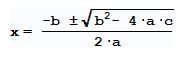


No hay comentarios:
Publicar un comentario